Скопировать ссылку на статью по ГОСТ 7.1-2003

УДК 681.32

О РЕШЕНИИ ОБРАТНОЙ ЗАДАЧИ КИНЕМАТИКИ ДЛЯ ПРОМЫШЛЕННОГО РОБОТА SCARA МЕТОДОМ НАХОЖДЕНИЯ БАЗИСА ГРЕБНЕРА

Аннотация

В работе рассмотрены методы компьютерной алгебры применительно к классическим задачам робототехники. Рассмотрено нахождение базисов Гребнера для решения систем алгебраических уравнений. Найдено алгебраическое решение обратной задачи кинематики для кинематической схемы четырехзвенного манипулятора типа ВВПВ с парами пятого класса.

Abstract

The paper discusses the methods of computer algebra applied to classical problems of robotics. Consider finding Gröbner bases for solving systems of algebraic equations. Found an algebraic solution of the inverse kinematics problem for the kinematic scheme of the four-arm type with pairs VVPV fifth grade.

Ключевые слова

Обратная кинематическая задача, базисы Гребнера, эквивалентное преобразование систем, промышленный робот SCARA.

Введение

Стремительное развитие вычислительной техники породило бурное развитие математической науки. На современном этапе сложились определенные вычислительные методы математики, доступные только при использовании ЭВМ. Одним из таких столпов современной алгебры – считается базис Гребнера идеала в кольце многочленов от многих переменных и приложение к решению систем нелинейных алгебраических уравнений.

Если на начальном этапе реализовывались эффективно только численные методы, то сейчас приоритетными являются аналитические или гибридные численно-аналитические методы. Венцом данной технологии стали известные широкому кругу ученых системы компьютерной алгебры $($от. англ. Computer Algebra Systems$)$. Это впервые позволило на ЭВМ решать, как классические, так и "нерешаемые" в недалеком прошлом задачи. Подробную исчерпывающую информацию по данной тематике можно найти в $[1]$, $[2]$ , $[3]$ .

Метод базисов Грёбнера и эквивалентное преобразование систем

Базисы Грёбнера идеалов в полиномиальных кольцах были открыты Б. Бухбергером в 1965 г. и названы им в честь В. Гребнера $($1899-1980$)$ – научного руководителя Бухбергера. Родственное понятие “стандартного базиса” идеала в кольце степенных рядов было независимо введено Х. Хиронакой в 1964 г. Термин “Базис Гребнера” используется в английском написании “Groebner base”. Теоретическая основа и современные методы этой технологии изложены в $[4]$ . Проиллюстрируем алгоритм работы базисов Грёбнера на задаче о решении системы алгебраических уравнений \eqref{eq:sample}:

\begin{cases} \begin{equation} \label{eq:sample} ab = c^2+ c\\ a^2= a + bc\\ ac = b^2+b \end{equation} \end{cases}

С помощью CAS Mathematica найдем базис Гребнера \eqref{eq:sample2} для системы \eqref{eq:sample}:

\begin{cases} \begin{equation} \label{eq:sample2} c^2(1+c) = 0\\ bc = 0\\ (b-c)(1+b+c)=0\\ (-1+a-c)c=0\\ ab-c(1+c)=0\\ (-1+a)a=0 \end{equation} \end{cases}

Согласно свойствам преобразования базисов Гребнера система \eqref{eq:sample} будет полностью эквивалентна системе \eqref{eq:sample2}. Преимущество преобразования \eqref{eq:sample} в \eqref{eq:sample2} очевидное. Первое и шестое уравнение преобразованной системы \eqref{eq:sample2} не зависят от оставшихся неизвестных, следовательно, легко находится все возможные решения. Для данного примера получаем следующие 4 решения: $\{a=0,b=0,c=-1\}$, $\{a=0,b=-1,c=0\}$,$\{a=0,b=0,c=0\}$, $\{a=1,b=0,c=-1\}$.

Обратная задача кинематики промышленного робота SCARA

Рисунок 1 – Промышленный робот Adept One

Рассмотрим промышленный робот типа ВВПВ SCARA компании Adept One $($рисунок 1$)$ с вращательными парами пятого класса, кинематическая схема которого приведена на рисунке 2.

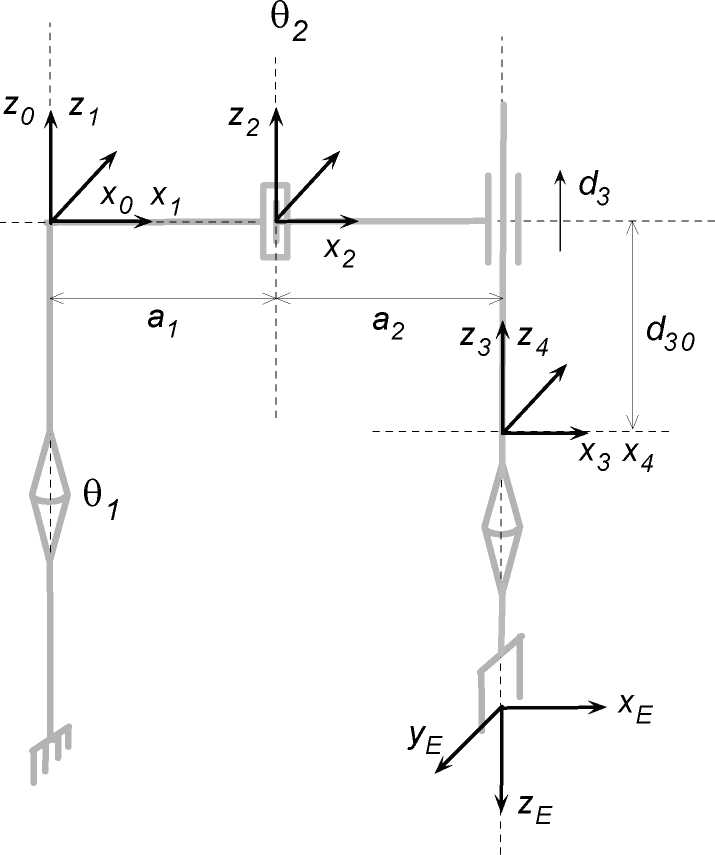
Рисунок 2 – Кинематическая схема робота Adept One

Классический вариант решения обратных задач кинематики $($определение обобщенных координат по заданной ориентации и координатам схвата манипулятора$)$ основан на перечислении всех возможных решений системы нелинейных тригонометрических уравнений $[5]$ . Представим параметры робота в виде таблицы 1, названной в честь Денавита и Хартенберга $[6]$ .

Таблица 1 – DH – параметры робота

Согласно данным, приведенным в таблице 1, решая прямую задачу кинематики получаем систему уравнений \eqref{eq:sample3}, где $s_1= sin(\theta_1)$, $s_2=sin(\theta_2)$

Для 1-го звена $^0_1T = \begin{bmatrix} c_1 & -s_1 & 0 & 0\\ s_1 & c_1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$ Для 2-го звена $^1_2T = \begin{bmatrix} c_2 & -s_2 & 0 & a_1\\ s_1 & c_1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$ Для 3-го звена $^2_3T = \begin{bmatrix} 1 & 0 & 0 & a_2\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & d_3-d_{30}\\ 0 & 0 & 0 & 1 \end{bmatrix}$ Для 4-го звена $^3_4T = \begin{bmatrix} c_4 & -s_4 & 0 & 0\\ s_4 & c_4 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}$ $$^0_4T = ^0_1T^1_2T^2_3T^3_4T = \begin{equation} \begin{bmatrix} \label{eq:sample3} s_1(c_4s_2+c_2s_4)+c_1(c_2c_4 - s_2s_4) & -c_1c_4s_2+s_1s_2s_4-c_2(c_4s_1+c_1s_4) & 0 & a_1c_1+a_2c_1c_2-a_2s_1s_2\\ c_2c_4s_1+c_1c_4s_2+c_1c_2s_4 & -c_1c_4s_2+s_1s_2s_4-c_2(c_4s_1+c_1s_4) & 0 & a_1s_1+a_2c_2s_1+a_2c_1s_2\\ 0 & 0 & 1 & d_3-d_{30}\\ 0 & 0 & 0 & 1 \end{bmatrix} \end{equation}$$

Обратная кинематическая задача вытекает из прямой и сводится к решению системы \eqref{eq:sample4}. Заметим, что значениями угла для 4 звена можно пренебречь при вычислении координат точки схвата, но оно необходимо при вычислении ориентации схвата:

\begin{cases} \begin{equation} \label{eq:sample4} a_1c_1+a_2c_1c_2-a_2s_1s_2 = p_x\\ a_1s_1+a_2c_2s_1+a_2c_1s_2 = p_y\\ d_3-d_{30} = p_z \end{equation} \end{cases}

При решении обязательно учитываем ряд особенностей:

1. При вычислении обобщенных координат $\theta_1$, $\theta_2$ нельзя пользоваться функцией arctan $($функция arctan не определена при значениях $\frac{-\pi}{2}, \frac{\pi}{2}$$)$.
2. Получить все возможные решения системы \eqref{eq:sample4} $($используются для оптимизации движения робота в задаче планирования траекторий$)$.
3. Получить необходимое и достаточное условие решения системы \eqref{eq:sample4} на всей области параметров.

Для решения системы \eqref{eq:sample4} выполним подстановку \eqref{eq:sample5}:

\begin{cases} \begin{equation} \label{eq:sample5} c_{1} = \frac{1-u^2_1}{1+u^2_1}\\ s_{1} = \frac{2u_1}{1+u^2_1}\\ c_{2} = \frac{1-u^2_1}{1+u^2_1}\\ s_{2} = \frac{2u_2}{1+u^2_2} \end{equation} \end{cases}

Применяя подстановку \eqref{eq:sample5} к системе \eqref{eq:sample4} получаем систему алгебраических уравнений \eqref{eq:sample6}

\begin{cases} \begin{equation} \label{eq:sample6} \frac{(-a_1+a_2)(-1+u^2_1)+4a_2u_1u_2+(a_1-a_2)(-1+u^2_1)u^2_2}{(1+u^2_1) (1+u^2_1)} = p_x\\ \frac{-2a_2(u_1+u_2)(-1+u_1u_2)+2a_1u_1(1+u^2_2)}{(1+u^2_1) (1+u^2_1)} = p_y\\ d_3-d_{30} = p_z \end{equation} \end{cases}

Найдем для системы \eqref{eq:sample6} базис Гребнера \eqref{eq:sample7}:

\begin{cases} \begin{equation} \label{eq:sample7} d_3-d_{30} - p_z = 0\\ (-a_1+a_2)^2 + p^2_x + p^2_y + (-(a_1 + a_2)^2+p^2_x + p^2_y)u^2_2 = 0\\ (a_1-a_2)^2 - p^2_x - p^2_y + \frac{4a_1a_2}{1+u^2_2} = 0\\ a^2_1(u_1-u_2) - (a^2_2 - p^2_x - p^2_y)(u_1+u_2)+2a_1(-p_y+p_xu_1+a_2u_2) = 0\\ a_1(u_1-u_2)+(a_2+p_x)(u_1+u_2)+p_y(-1+u_1u_2)=0\\ a_1+a_2-p_x+(a_1-a_2+p_x)u_1u_2-p_y(u_1+u_2) = 0\\ -p_y+(a_1-a_2+p_x)u_1+ \frac{2a_2(u_1+u_2)}{1+u^2_2} = 0\\ -a_1p_x + \frac{-(p^2_x+p^2_y)(-1+u^2_1)(1+u^2_2)+a_2(1+u^2_1)(-2p_yu_2+p_x(-1+u^2_2))}{(1+u^2_1)(1+u^2_2)} = 0\\ -a^2_1+p^2_y-\frac{2a_2(-1+u^2_1)(p_x-p_yu_2)}{1+u^2_1}-p_x(p_x+2p_y)-\frac{(2a_1(a_2(1+u^2_1)+(-1+u^2_1)(p_x-p_yu_2))}{1+u^2_1}+ a^2_2(3-\frac{4}{1+u^2_2})=0\\ 2p_y(a_1+a_2+p_x- \frac{2(a_1+a_2)}{1+u^2_1}) - \frac{((-a_1+a_2+p_x)^2)-p^2_y+((-a_1+a_2+p_x)^2-p^2_y)u^2_1)u_2}{1+u^2_2}+\frac{4a^2_2u_2}{1+u^2_2}=0\\ \frac{(a_1+a_2)(a_1+a_2-p_x-(a_1+a_2+p_x)u^2_1)-2a_2p_y(1+u^2_1)u_2-(a_1+a_2)(-a_1+a_2+p_x-(a_1-a_2+p_x)u^2_1)u^2_2}{1+u^2_1}=0\\ \frac{-4a^2_2(1+u^2_1)u^2_2+a_1p_x(-1+u^2_1)(1+u^2_2)+p^2_x(1+u^2_1)(1+u^2_2)-a_2(-1+u^2_1)(1+u^2_2)(2p_yu_2+p_x(-1+u^2_2))}{(1+u^2_1)(1+u^2_2)} = 0\\ -2p_xp_y+a^2_1u_2-p^2_xu_2-p^2_yu_2+a_1(p_y(-2+ \frac{4}{1+u^2_1})-2a_2u_2) - \frac{2a_2(-1+u^2_1)(p_y+2p_xu_2-p_yu^2_2)}{(1+u^2_1)(1+u^2_2)}+ \frac{a^2_2u_2(-3+6u^2_2+u^4_2)}{(1+u^2_2)^2}=0\\ -a_1+a_2-p_x+ \frac{2(p_x+p_yu_1)}{1+u^2_1}-\frac{2a_2}{1+u^2_2} = 0\\ \frac{2(a_1+a_2)u_1-p_y(1+u^2_1)+(-a_1+a_2+p_x+(a_1-a_2+p_x)u^2_1)u_2}{1+u^2_1}=0\\ p_y+ \frac{2(-p_y+p_xu_1)}{1+u^2_1}+\frac{2a_2u_2}{1+u^2_2}=0\\ \frac{a_1(-1+u^2_1)(1+u^2_2)+p_x(1+u^2_1)(1+u^2_2)+a_2(-1+u^2_1+4u_1u_2+u^2_2+u^2_1u^2_1)}{1+u^2_1}=0 \end{equation} \end{cases}

Заметим, что система \eqref{eq:sample7} проще \eqref{eq:sample6}. Например, \eqref{eq:sample2} уравнение зависит только от $u_2$. Решая систему \eqref{eq:sample7} получаем 2 решения:

\begin{cases} u_1 = \frac{2a_1p_y-\sqrt{(a_1-a_2)^2-p^2_x-p^2_y}\sqrt{-(a_1+a_2)^2+p^2_x+p^2_y}}{-a^2_2+(a_1+p_x)^2+p^2_y}\\ u_2 = \frac{\sqrt{-(a_1+a_2)^2+p^2_x+p^2_y}}{\sqrt{(a_1-a_2)^2-p^2_x-p^2_y}}\\ d_3 = p_z+d_{30} \end{cases} \begin{cases} u_1 = \frac{2a_1p_y+\sqrt{(a_1-a_2)^2-p^2_x-p^2_y}\sqrt{-(a_1+a_2)^2+p^2_x+p^2_y}}{-a^2_2+(a_1+p_x)^2+p^2_y}\\ u_2 = \frac{\sqrt{-(a_1+a_2)^2+p^2_x+p^2_y}}{\sqrt{(a_1-a_2)^2-p^2_x-p^2_y}}\\ d_3 = p_z+d_{30} \end{cases}

Зная значения промежуточных переменных можно легко найти косинусы и синусы соответствующих углов. С помощью специальной функции по значениям синуса и косинуса углов легко определяются обобщенные координаты.

Заключение

На примере кинематических уравнений четырехзвенного манипулятора продемонстрированы современные символьные вычислительные методы систем компьютерной алгебры. Решения, полученные выше, найдены в параметрах робота без привязки к заводским значениям величин $a_1$, $a_2$, $d_{30}$, однозначно определяют все возможные конфигурации робота и предназначены для реализации в системе управления роботом. Необходимо отметить, что такая проработка вопроса обратной кинематики проведена для возможности оперативного и точного расчета конфигураций в режиме реального времени для задач планирования траектории и движения. Аналитический поиск необходимого и достаточного условия c помощью систем компьютерной алгебры изложен в $[7]$ .

Список использованных источников