АНАЛИТИЧЕСКИЙ ПОИСК НЕОБХОДИМОГО И ДОСТАТОЧНОГО УСЛОВИЯ С ПОМОЩЬЮ СИСТЕМ КОМПЬЮТЕРНОЙ АЛГЕБРЫ

Существенным прорывом в области современной математической науки, оперирующей символьными методами, являются системы компьютерной алгебры. Их область применения постоянно расширяется, а функциональные возможности совершенствуются и дополняются. Это позволяет на обыкновенных персональных компьютерах решать быстро как классические, так и "нерешаемые" в недалеком прошлом задачи $[1]$, $[2]$, $[3]$, $[4]$. Подробную современную информацию по данной тематике можно найти в $[5]$, $[6]$.

При реализации любых моделей на ЭВМ, использующих аналитические решения, для отброса некорректных данных нужно иметь необходимое и достаточное условие существования решения.

Для пояснения приведем простой пример иллюстрирующий, что именно CAS Mathematica находит для такого рода задач.

Найти необходимое и достаточное условие для уравнения \eqref{eq:sample1}

\begin{equation} \label{eq:sample1} |x| + |y| = 1 \end{equation}

Геометрическое решение данной проблемы приведено на $($рис. 1$)$

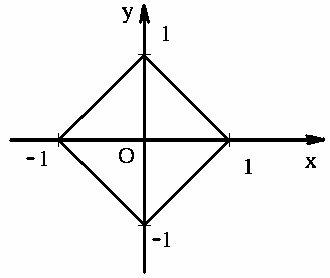
Рисунок 1 - Геометрическое решение

Необходимое и достаточное условие найденное CAS Mathematica \eqref{eq:sample2}

\begin{equation} \label{eq:sample2} y = 0 \land (x = -1 \lor x = 1)) \lor (-1 \lt x \le 0 \land (1 + x + y = 0 \lor 1 + x = y)) \lor (0 \lt x \lt 1 \land (x + y = 1 \lor x = 1 + y)) \end{equation}

, где по аналогии с языком программирования С \eqref{eq:sample3}: \begin{equation} \label{eq:sample3} \land - логическое\;И\\ \lor -\;логическое\;ИЛИ \end{equation}

Список использованных источников